Basic Stats - Descriptive Stats: Central Tendency, Divergence and Distributions

Descriptive Stats

Descriptive stats is the area of stats used to describe general summary information about data. These stats basically describe something about the middle values of the data and how the data varies.

NOTE: in this blog the measures discussed are specifically for numeric rank order data. The generally do not apply to categorical data such as:

• Color - Color eyes, hair, objects
• Numerical Categories - Zip Code, Social Security Number, account number.
• Type of Object - car brand, type of car, type of house, ...

Central Tendency

The first concept that one needs to deal with in basic Stats is the concept of Central Tendency.

This seems like a simple concept, and it really is, but there are a few subtleties. When we talk about central tendency, we usually think of average, but what is average really? There are several things people refer to when they talk about the average:

Average - The classical definition in stats is called the Mean which is the sum of all values divided by the number of values. For example, if you have 10 people in a room and you add their ages and you get 100 then the average or Mean age of this group is 10 years.

Median - Sometimes, when people say average, they really mean the Median, which is the middle value. This is obtained by ranking the observations in numerical order and then picking the middle value (if you have an even number of values you take the mid point between the middle two values). For example, in our hypothetical room lets say you have, 5 four year-olds, 4 five year-olds and one 55 year-old. The middle value is then 4.5 years. Average is often represented by the symbol X with a line over the top, called X-bar.

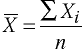
Mode - The mode is the most common value. In our room, the mode would be  years.

As can be seen in this example, there is a huge difference between Mean and Median and Mode. Because of this it is important to know what someone (especially someone with an Agenda) means when they refer to average. This is particularly true when the value being used is from a "skewed" distribution where most the observations are in a narrow range, but a few are substantially different. Typically, this causes the Mean to be significantly different from the Median.

This is especially true of Income. For example, lets say the company for which you work has 100 people and 95 of them make minimum wage of $8.00 per hour. The remaining 5 managers make $100, $200, $300, $400, and $500 per hour. Here, the Median wage ($8.00) might be quoted if someone wanted to imply that the company didn't have a very high payroll, but if another person wanted to brag about how well paid the employees were they might use the Mean ($13.60). So if someone said the average worker at this company makes X dollars and hour, what value should they use?

Divergence

In the discussion above on central tendency, I referred to a "skewed" distribution. This starts to get into the concept of divergence.

Divergence is an extremely important concept in stats.To demonstrate this let's take an example from American football. As a coach, you are in a situation where you need to gain at least 1 yard. You need to chose between two plays. Looking at the stats you see that both plays gain an average of 2 yards; however, play A gains 2 yard plus or minus 1 yard and play B most of the time loses ground, but sometimes gains 10 or more yards. The choice should be obvious, for this situation you should call play A.

In this example, Play A has a much smaller divergence than Play B. In a different situation, say where 10 yards is required, play B might be more appropriate.

As with central tendency, there are a number of divergence calculations:

Variance - This stat is rarely mentioned in descriptive stats, but it is one of the basic calculations. It is defined as the sum of the squared differences between each value and the mean. It is represented by s squared:

Standard Deviation - This is the most common calculation and is the square root of the variance:

Why do we use standard deviation? It all gets down to some higher level math and the convenience of the variance calculation. For basic description, it is best to think of the average absolute deviation.

Average Deviation - An easier to understand calculation is the average absolute deviation (we use absolute deviation because basic deviation is positive and negative and would average out to zero). For the average deviation add up the absolute deviation for each observation from the mean and then take the average of those values:

Other measures of divergence are:

Range - The difference between the largest and smallest value.

Inter-Quartile Range - The range of the middle 50% of the population.

There are a number of other divergence calculations, but they are relatively esoteric and beyond the scope here.

Distribution

When we describe a distribution we generally talk about the shape of the curve that describes the data. These distributions fall into three basic categories:

Normal Distribution - This is the classic symmetric, bell shaped distribution:

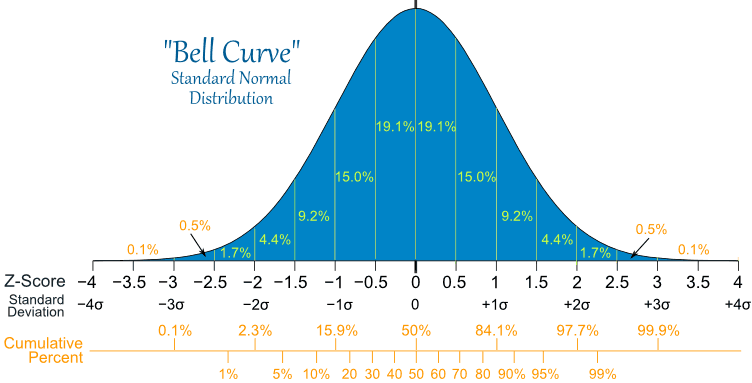
Typical normal distributions are physical measurements, such as weight, height, distance, speed, ...

• Uniform - This is basically a flat distribution. All values are equally frequent. A good example is the number (1-6) on a fair single die. 
• Symmetric - The unifom and Normal distributions are symmetric, there are also other symmetric distributions that may be flatter or wider than a typical Normal distribution.
• Skewed distributions - In the example used in the Central Distribution discussion above, we saw a skewed distribution where the distribution is NOT symmetric.
  
  

Knowledge of the type of the distribution is helpful in understanding both the importance of the measure used for central tendency and dispersion.

For symmetric distributions, the Mean, Median, and Mode are about the same and the dispersion measure tells you about how far the data are spread on either side of the middle. For skewed distributions there are significant differences between the central tendency values:

Summary

As a data consumer, which everone is, knowledge of the basics of descriptive stats are important when reading, watching, or listening to various reports in the media (news reports, advertisements) it is important to question the assumptions on which these reports are based. 

• Is the reported middle value from a skewed distribution?
• Are they reporting mean, median, or model?
• What is the dispersion of the data being reported? 
• Does the middle value come from data with a narrow distribution or a large dispersion?